您现在的位置是:主页 > 理科竞赛 > 数学竞赛 >
AMC8冲全球1%,吃透30大知识点+掌握12大题型
发布时间:2024-01-19 20:56:30浏览量:次
摘要:AMC8竞赛作为低龄数学竞赛的天花板,它的含金量非常高,同时知识范围也非常广。对于6年级及以下的学生来说,需要补充大概30%的7-8年级的知识点。为了方便各位学生更好地备考,我
AMC8竞赛作为低龄数学竞赛的“天花板”,它的含金量非常高,同时知识范围也非常广。对于6年级及以下的学生来说,需要补充大概30%的7-8年级的知识点。为了方便各位学生更好地备考,我整理了AMC8竞赛30大知识点和12大题型,供参考学习。

组合考点:
枚举法
加减法计数《容斥原理标数法》
乘法计数与排列数
组合数
基本计数策略(分类讨论算反面)
概率问题
组合问题的难度较高,AMC8的组合问题通常数量在15%左右,其中有些AMC10级别的组合问题会作为AMC8的压轴问题出现,但不会过多考察同学的概率部分,而是重点考察组合学。
数论考点
质数与合数
倍数与因数
质因数分解
整除法则
余数问题(求余数方法)
位值原理
特殊数(次方数阶乘回文数)
数论部分考察内容比较灵活,AMC8考试中一般会涉及到15%-20%的此类问题, 不过这部分知识单纯的从概念学习并不能很好掌握,而是需要通过系统的学习和练习相辅相成才会明白数论问题的解决思路,通常是由概念引出的一些思维的。
几何考点
勾股定理
全等与相似三角形
特殊多边形
圆
面积问题(切割法、面积模型等)
角度问题
立体几何
几何部分在AMC8数学竞赛中占比大约20%-30%左右,考察内容相对比较灵活,但不会涉及到比较复杂的几何结合计算问题,但同样也要求同学们对几何问题有着自己的直观理解和分类
代数考点
算数运算
代数式的运算
开根号解二次方程
因式分解
一次函数
数列问题
不等式问题
代数是AMC数学竞赛重点考察模块,在正式考试中占比比较大,大约在35-45%左右。需要同学们在备考过程中重点关注。 这部分内容主要考察同学的细心程度,更多的还会从问题中讲述应用问题背景,向同学传达一些需要建模的数学问题,如很经典的小车相向而行、同向而行计算相聚时间等等,这也要求同学具备一些生活常识与物理常识。
应用题考点
比例与百分比问题
比率问题(例行程问题等等)
逻辑问题
统计(平均数、中位数 、众数、极差)
图表问题
最值问题
百分数问题
学习要求:熟练掌握百分数、分数及小数的计算及其相互转化
考察内容:百分数计算问题、百分数、分数绩效书的多步骤计算、比较大小等
统计与概率问题
学习要求:需要掌握复杂情形下的概率计算
考察内容:统计基本概念,比如求解mean平均数、mode众数、median平均数等,同时也会考察对常见统计图表的综合分析解读能力,难度比较大
估值计算问题
学习要求:考察学生对数字保留适当的有效位进行估值计算
考察内容:对数字的估值计算,不可以使用计算器
基本代数概念问题
学习要求:需要熟练掌握
考察内容:基本代数概念问题。比如因数、倍数、比例等
初等几何问题
学习要求:需要对中学阶段的几何基本概念及其性质熟练掌握, 一般题目会综合考察
考察内容:初等几何,包括平面多边形、圆的面积和周长以及勾股定理等
空间可视化问题
学习要求:重点考察空间想象能力和分析解决问题能力
考察内容:利用空间立体图形来出题
情景应用题
学习要求:需要仔细阅读,情景和数学结合
考察内容:结合生活实际情景出题,难度不大
找规律题
学习要求:考察解决问题的能力
考察内容:考察根据题目给出特定情形分析推理出变化规律
推理分析类问题
学习要求:需要会使用多方法综合分析推出结论,比如分类法、逆推法
考察内容:考察分析推理、逻辑思维能力
排列组合问题
学习要求:需要熟练掌握
考察内容:排列组合,难度中等
方程问题
学习要求:需要熟练掌握
考察内容:包含一次方程、线性方程组、二次方程等
几何坐标问题
学习要求:一般较为综合
考察内容:结合平面图形以及常见代数问题综合考察
课程对象
1、3-5年级或具备3-5年级水平
2、少部分2年级但具备3年级水平的同学
3、要求熟练掌握整数的四则运算,规则图形的周长面积计算
4、想参加AMC8考试的学生
课程目标
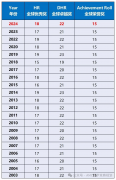
AMC8低龄成就奖(15分奖)