AMC8竞赛都考哪些内容？对应校内几年级的数学知识？

MC8都考哪些内容呢？往年知识点都是怎么分布的？AMC8和学校学习的知识点一样吗？重合度高吗？我今天一 一给大家解答。

 

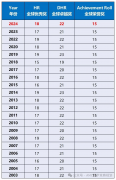
AMC8竞赛真题知识点分布

 

 

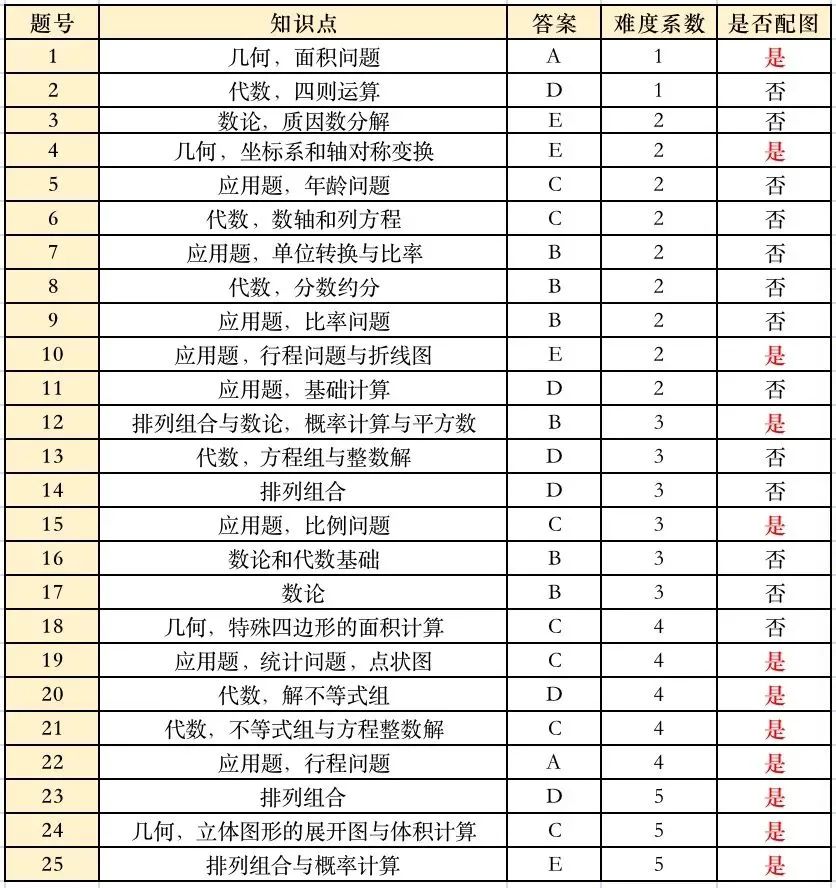
AMC8竞赛7大高频考点

 

计算部分

大多有实际应用背景，类似应用题，涉及分数、百分数、小数计算，但是复杂程度较低。考察学生的计算能力，在算题目的时候不能马虎。

应用题部分

主要涉及应用问题，行程问题，逻辑推理问题。考察学生理解题目的能力，和每种问题的解题方法，例如：应用问题像假设法、分组法；行程问题像比例关系、平均速度、分段与比较；
逻辑推理像排除法、假设法、列表画图法、特殊值法。

几何部分

较多涉及空间想象、圆与扇形、勾股定理等内容，不涉及复杂的三角形相关的比例关系。这部分对于考生来说是重难点，要熟悉常见平面图形的面积，周长公式和算法。还有求不规则图形面积的方法，包括拆分法、割补法等。由于考生年级在八年级以下，对于圆或勾股定理等知识不熟悉，要多加学习。

 

计数部分

涉及较多的排列组合，容斥原理、加法原理、乘法原理等内容。其中计数原理要了解加法和乘法的区别，加法计数原理的关键词是分类，乘法中的关键词是分步。

 

组合数学

涉及初步的逻辑推理，通常使用列表辅助即可解决，此外还会涉及奇偶性分析。

 

数论部分

涉及较为初步的质数与合数、约数与倍数、整除问题、余数问题，多次考察了位值原理。数论部分中概念比较多、容易混淆，所以在复习的时候首先要弄清楚每部分内容的概念与性质和计算方法。

 

其他考点内容

图表理解、统计、概率、勾股定理。

 

AMC8考点对应校内数学知识

 

 

 

 

课程大类	名称	校内数学占比	年级
逻辑	逻辑推理	5%	4-6年级
代数	基础运算	20%	3年级
	分数，比例，比率，比例式和百分比		3-6年级
	进阶运算		5-7年级
	行程问题		3-5年级
数论	奇数和偶数	15%	3-4年级
	数的整除性		4-6年级
	质数		5年级
	分解质因数		6-7年级
	最大公因数和最小公倍数		4-5年级
	余数		2-5年级
计数和概率20%	排列	20% 15% 25%	5-8年级
	组合		5-8年级
	概率		5-7年级
	计数		3-6年级
	集合和韦恩图		3-6年级
	数据的描述		3-5年级
代数二	等差数列		3-5年级
	等比和递推数列		4-6年级
	解方程		3-5年级
	列方程		4-6年级
	不定方程		5-6年级
几何	角和线		3-4年级
	三角形(一)		4-6年级
	三角形(二)		5-8年级
	四边形和多边形		3-6年级
	圆		5-6年级
	直线和圆的方程		5-7年级
	解析几何		6-7年级
	立体几何		4-6年级

 

AMC8秋季冲刺班课程

 

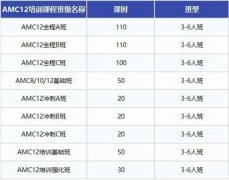
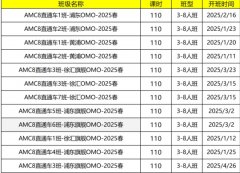
Pre-AMC8秋季课程

 

Pre AMC8针对3-4年级学员，侧重学习小学数学+小学奥数6大重要模块

 

入班要求

1、3-4年级或具备3-4年级校内水平

2、要求熟练掌握整数的四则运算，规则图形的周长面积计算

 

课程目标

AMC8低龄成就奖(15分奖)
 

AMC8秋季班课程

 

AMC8课程针对5-7年级有一定基础的学生，开设基础班、强化班、冲刺班等，通过测试孩子的基础情况，分层教学。

 

课程目标

 

AMC8全球前1%和前5%奖项