低年级学生参加AMC10获奖率如何？

美国数学奥赛晋级比赛包括：AMC8，AMC10/12→ AIME→ USAJMO/USAMO美国数学奥林匹克竞赛→ IMO国际数学奥林匹克竞赛

AMC10竞赛基本信息

参赛资格：10年级或以下，且年龄不超过17.5岁

竞赛时长：75分钟

竞赛题型：25道单项选择题

竞赛时间：每年11月份（具体时间以官方通知为准）

计分方式：答对一题得6分，不答得1.5分，答错得0分，满分150分。

 

AMC10竞赛知识点

 

 

主题	内容	考察点
代数综合	主要涉及数列，方程，二次函数，不等式，乘法公式等	重点考察学生对知识点的掌握及分析问题的能力，难点在于简化问题以及多项式和二次函数整除根问题的解法
函数部分	主要涉及坐标系，位置变换，一次函数，圆的方程	重点考察学生理解题目的能力，和每种问题的解题方法。难点在于求多边形面积，可灵活运用皮克定理和鞋带定理
几何综合 三角形,四边形,多边形	主要涉及三角函数，相似和全等，三角形相关定理以及面积计算的多种方法。	这部分要熟悉三角函数公式和算法，还有不规则图形面积的方法，包括割补法，等面积替换等。
几何综合 圆与立体几何	主要涉及圆的性质和立体几何的提及，表面积以及欧拉公式。	难点在于圆的相关定理如圆周角定理等，主要考察学生空间想象能力和做辅助线能力。
排列组合	主要涉及来加乘原理，单循环赛制，排列组合等内容。	主要考察学生分析情景的能力，对于复杂组合问题。
概率统计	主要涉及各种统计量以及古典概率和几何概型等。	难点在于条件概率。主要考察学生对于各种事件可能发生情况的分析能力。
数论部分	主要涉及因数与倍数，数位，质数与合数等。	难点在于奇偶性分析，取余取整以及定义新运算问题。这一部分一般较难，通常出现在后几题。

 

低龄学生参加AMC10获奖率高吗？

 

很多家长问：我的孩子目前处于低年级（以6-8年级为主）阶段，参加AMC10有没有机会得奖？

 

首先要声明一点，对处于低年级（以6-8年级为主）的大部分同学来说，AMC8较AMC10来说才是最合适的竞赛，因为想从AMC10晋级AIME，意味着至少在考试里，必须赢下95%的考生，其中不仅仅是同龄人，可能还包括越级挑战高年级学生。

 

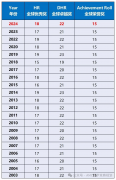
但我们分析历年的获奖数据，出乎意料的是仍然有近30%的获奖学生属于6-8年级。

 

6年级	2.9%
7年级	8.2%
8年级	17.2%
9年级	29.8%
10年级	42.0%
年级	获奖比例

 

对AMC10来说，在代数和几何方面，考察的就是理解和应用。

 

代数的学习：从数➡字母➡代数式➡方程➡函数，是以一个比较漫长的过程。

 

几何的学习：从线与角➡四边形➡三角形➡全等➡相似，也是一整套过程。

 

每一个后面的环节都需要前面的环节做铺垫，如果说前面的知识有遗漏，或者说掌握的不是很牢固，后面肯定也会出问题，建议在参加比赛前，先把知识点学扎实。

 

低龄学生通过AMC10晋级AIME需补充哪些知识？

 

孩子如果刚刚接触数学竞赛且是6年级及以下学生，建议孩子从AMC8开始学起，打好数学学习基础。

 

孩子如果是6-8年级且有一定数学竞赛经验，可以让孩子开始备考AMC10，同时参加AMC8竞赛。

 

数学竞赛学习强调是循序渐进，通过参加AMC竞赛，让孩子提升数学思维，感受数学乐趣，最终促进孩子校内数学的学习。所以AMC8与AMC10备考选择，还是要根据孩子自身数学基础来进行

 

AMC8衔接AMC10需要补充的知识点如下：

 

数列：

① 两种基本数列：等差数列和等比数列

② 等差数列与等比数列的通项公式，递推公式及求和

③ 复杂的等差数列与等比数列的应用

④ 非等差和非等比数列的计算

 

线性函数：

① 线性函数的图像，性质及解析式

② 线性不等式的求解及应用

③ 直线在坐标系的计算和应用

④ 列线性方程解应用题

 

排列组合及概率：

① 计数基本法则：乘法法则和加法法则

② 排列的原理和应用

③ 组合和应用

④ 概率的计算法则及其应用

 

整体运算：

① 最大公约数，最小公倍数

② 连续整数，奇数和偶数的求和及乘积

③ 各种因式分解的方法及其广泛的应用

④ 指数运算的基本法则及解方程

 

2024AMC8/10全程班安排

 

第一阶段，夯实知识点（50小时）

单个的知识点的学习与深入挖掘，夯实学校不讲的但是竞赛会考的知识点，并制作了对应的分类习题库，定位你的学术短板。

 

第二阶段，串联知识点（30小时）

完成专题的训练，知识点的串联，锻炼数学思维和学习方法。

 

第三阶段，模考与冲刺（30小时）

模拟考试点评，锻炼学生做题的节奏感，及如何分配精力做题，甚至包括该怎么使用草稿纸。